5.4. Plotting i SymPy#

Vi kan tegne grafer for funktioner og udtryk ved hjælp af SymPy. Det mest grundlæggende værktøj er funktionen plot, som vi importerer fra sympy.plotting her:

# Den anbefalede standardblok for SymPy:
import sympy as sp                    # Importer sympy
from sympy.abc import x               # Vi vælger at importere x som symbolsk variabel.

# Specifik import til plotteformål:
from sympy.plotting import plot

For at komme i gang vil vi gerne tegne grafen for en sinuskurve og definerer derfor først sinus som et udtryk:

expr = sp.sin(x)

og tegner derefter ved at bruge funktionen plot.

plot(expr);

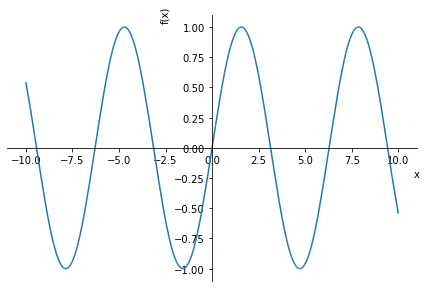
Tip: Bemærk semikolonet, der beder Python om ikke at skrive outputtet, som her ville være en kode i stil med sympy.plotting.plot.Plot at 0x136af246608, som ikke er så relevant i denne kontekst.

Hvis man ønsker at tegne grafen for et bestemt $x$-interval, skriver man plot(udtryk, (variabel, start, slut)). Eksempel:

from sympy import pi
plot(expr, (x, 0, 2 * pi));

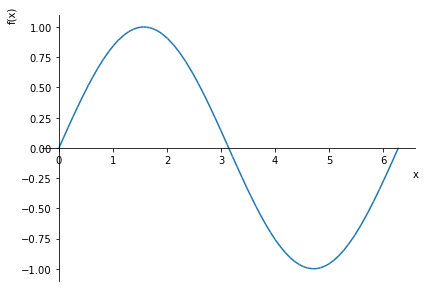
Man behøver naturligvis ikke at definere udtrykket først som en variabel, men kan skrive funktionen eller udtrykket direkte ind i plot. Hvis man ønsker at lave flere grafer i samme figur, kan man skrive plot(udtryk_1, udtryk_2, (variabel, start, slut)) som det fremgår her:

plot(sp.sin(x), sp.cos(x), (x, 0, 2*pi));

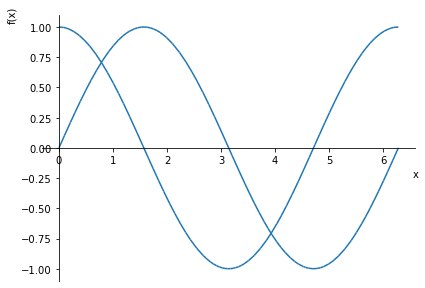
5.4.1. Parametre for Plot#

Udover at angive funktionen/udtrykket og afgrænsningen af den variable, kan man til plot angive en del andre oplysninger, som angives ved at tilføje keyword = værdi i slutningen af udtrykket. Nogle hyppigt anvendte keywords er:

title angiver titlen på figuren. Angiv værdien som en string, altså som “Ønsket titel”
legend angiver om der skal stå en beskrivelse af graferne. Angiv i så fald værdien True
line_color giver grafen en bestemt farve. Angiv værdien som en string, der indeholder en standardfarve, eksempelvis “red”, “green”, eller som en RGB-farvekode (r, g, b), hvor de tre værdier er mellem 0 og 1
xlim og ylim fastlægger aksernes afgrænsninger i hhv. vandret og lodret retning. Angiv to værdier (fra, til) for hver akse.
xlabel og ylabel sætter navne på hhv. $x-$ og $y-$akse. Angiv som string.

Andre keywords kan findes i dokumentationen her

Tip: Når vi angiver tekststrenge på et plot, kan vi skrive r"$LaTeXkode$" hvis vi gerne vil have LaTeXkode formatteret ved hjælp af Latex. r betyder, at tekststrengen skal læses rå og ikke som Python normalt ville fortolke teksten (f.eks. giver \n et linjeskift i Python). At kunne bruge LaTeX er særligt praktisk når man vil bruge græske bogstaver som variable.

Med disse muligheder kan vi forbedre vores seneste figur:

plot(sp.cos(x), sp.sin(x), (x, 0, 2*pi), 
     title = "Harmoniske svingninger", 
     legend = True, 
     xlabel = r"$x$", 
     ylabel = 'Amplitude');

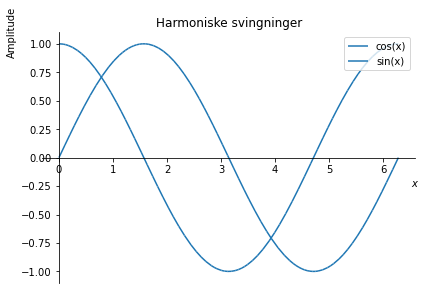
Tip: Bemærk her, at vi opdeler et funktionskald på flere linjer ved at indsætte linjeskift efter , for at gøre koden mere overskuelig.

Den kompakte kommando til plotning af to grafer tillader desværre ikke umiddelbart at vi giver dem forskellige farver. For at gøre det, kan vi gemme selve figuren som et objekt med et navn ligesom en variabel, hvorefter det er muligt at ændre på de forskellige indstillinger. Vi benytter her show = False til ikke at vise vores plot, mens vi stadig redigerer det. Når vi er klar til at vise plottet, skriver vi figur.show().

# Vi tegner en graf og navngiver resultatet som et objekt ved navn "figur"
figur = plot(sp.cos(x), 1.5*sp.sin(2 * x), (x, 0, 2*pi), show = False)

Når vi vil ændre indstillingerne for en eksisterende graf, gøre dette ved at skrive:

figurnavn.keyword = ny_værdi

Dermed kan vi nu sætte labels, titler og tilføje en legend ved ligesom overstående at skrive:

# Overordnet til hele figure:
figur.legend = True
figur.title  = "Forskellige harmoniske svingninger"
figur.xlabel = r"$x$"
figur.ylabel = r"$A(x)$"

Indstillingerne til de enkelte grafer er elementer i en liste, så for at ændre indstillingerne for det i’te plot (husk nulindeksering, så den første kurve er nummer 0), skriver vi:

figurnavn[i].keyword = ny_værdi

Vi kan altså ændre på de to plots seperat ved at gøre følgende:

figur[0].line_color = 'red'  # Der er flere kurver i figuren, og hver af dem har en farve. 
                             # Kurverne har nummer 0, 1, 2, ... i den rækkefølge, de blev tegnet, så cosinus-kurven er 0

figur[1].line_color = (0.6, 0.4, 0.2)  
                             # ... og sinus er nummer 1. Her bruges RGB-farvekode. Farven er brun!
figur[1].label      = r"$\frac{3}{2} \sin(2 x)$"

Efter at have ændret indstillingerne, beder vi Python om at vise figuren:

figur.show()

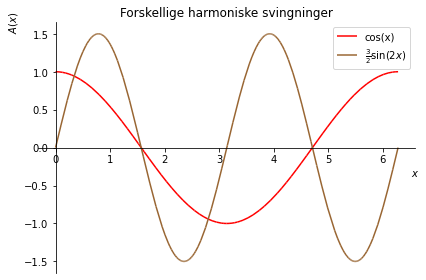
5.4.2. Figurer som lister#

I overstående eksempler har vi benyttet indeksering (som vi kender det fra lister) til at ændre på forskellige parametre. En af fordelene ved dette er at vi kan udvide vores figur ved brug af .append() og .extend() til at bygge videre på en figur, hvis vi ønsker at samle flere plots i en figur. Som eksempel vil vi bruge .append() til at tilføje en ekstra kurve til overstående figur.

f = sp.cos(2*x/3)

figur2 = plot(f, (x, 0, 2 * pi), line_color = 'orange', legend = True)

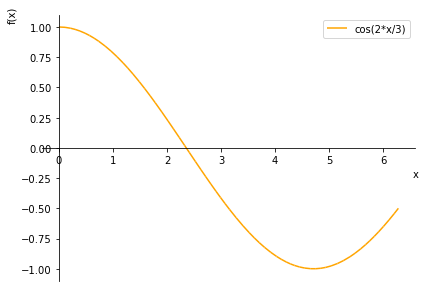
Denne kurve har nu fået objektnavnet figur2[0] fordi det er den første kurve i figuren, og vi kan nu tilføje den til figur ovenfor ved hjælp af append:

figur.append(figur2[0])
figur.show()

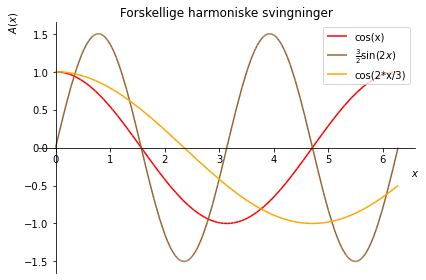
Hvis man vil kombinere figurer, som alle har flere kurver, kan man bruge .extend() til at tilføje alle plots fra en figur til den anden. Hvis figur2 således havde haft 2 kurver, ville vi kunne tilføje begge til figur ved at skrive

figur.extend(figur2)

5.4.3. Gaffelfunktioner#

Hvis vi ønsker at lave stykvis definerede funktioner, der har forskellige funktionsudtryk i forskellige intervaller (også kendt som “gaffelfunktioner”), kan vi benytte sp.Piecewise(). Kaldesekvensen er:

sp.Piecewise((udtryk1, intervalbetingelse1), (udtryk2, intervalbetingelse2))

Funktionen:

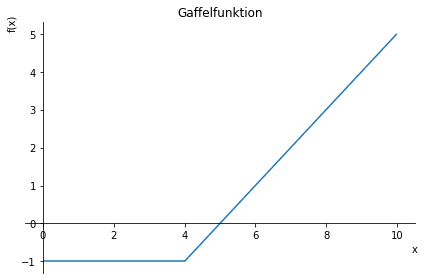
$f(x) = \begin{cases} -1 \quad &x < 4 \\ x - 5 \quad &x \geq 4\end{cases}$

angives derfor som

f = sp.Piecewise((-1, x < 4), (x-5, x >= 4))

figur3 = plot(f, (x, 0, 10), title = "Gaffelfunktion")

sp.Piecewise kan arbejde med et større antal udtryk og intervalbetingelser end blot to som i eksemplet. Hvis nogle $x$-værdier opfylder flere af intervalbetingelserne, anvender SymPy det første udtryk hvor et givet $x$ opfylder betingelsen. Man kan bruge dette på en smart måde, hvis man skal tegne en gaffelfunktion, hvor samme funktionsudtryk gælder i flere intervaller for $x$. Man kan eksempelvis lade det andet udtryk gælde alle steder, hvor den første ikke gælder, ved blot at angive andet udtryks intervalbetingelse som True og angive det som det sidste udtryk. Et eksempel på dette kunne være at betragte gaffelfunktionen:

$g_1(x) = \begin{cases} -2x \quad &x < -2 \\ x^2 \quad &-2\leq x\leq 2\\ 2x \quad &2 < x\quad \end{cases}$

som kan skrives kortere som:

$g_2(x) = \begin{cases} x^2 \quad &|x|\leq 2\\ 2|x| \quad &\mbox{ellers}\end{cases}$

På samme måde kan denne funktion defineres i Python på 2 ækvivalente måder:

g1 = sp.Piecewise((-2*x, x<-2), (x**2, abs(x) <= 2),(2*x, x>2))
g2 = sp.Piecewise((x**2, abs(x) < 2),(2*abs(x), True))  

Bemærk at vi for andet udtryk med vilje ikke skriver nogen betingelse for x, men blot ‘True’, som altid er opfyldt, idet vi ønsker at bruge det andet udtryk når betingelsen for første udtryk (abs(x)<=2) ikke er opfyldt.

Plotter vi nu de to kurver (her separeret visuelt ved at vi har lagt en konstant til den ene), får vi:

figur = plot(g1, g2 + 1, (x, -5, 5), title = "Gaffelfunktion 2", show = False)
figur[0].line_color = "blue"
figur[1].line_color = "orange"
figur.show()

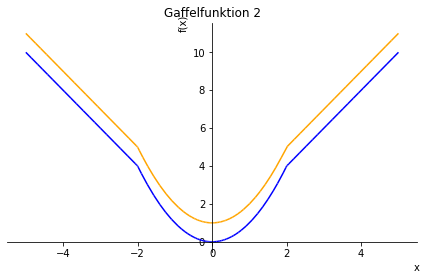
Hvilket viser at de to notationsmetoder som forventet giver samme resultat.

Angives udtrykkene derimod i omvendt rækkefølge, kommer udtrykket $x^2$ aldrig i brug, da betingelsen True altid er opfyldt, og det er blot abs(x), dvs. $|x|$, der tegnes

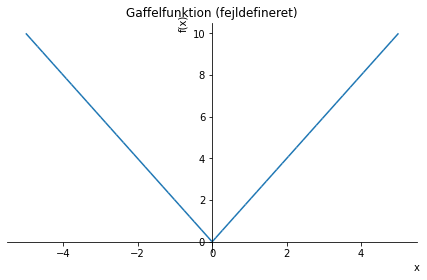
g = sp.Piecewise((2*abs(x), True), (x**2, abs(x) < 2))

figur = plot(g, (x, -5, 5), title = "Gaffelfunktion (fejldefineret)")

Python i LinAlys og MekRel

Plotting i SymPy

Contents

5.4. Plotting i SymPy#

5.4.1. Parametre for Plot#

5.4.2. Figurer som lister#

5.4.3. Gaffelfunktioner#