Komplekse tal i SymPy
Contents
5.12. Komplekse tal i SymPy#
I LinALys lærer du at regne med komplekse tal. SymPy kan være en hjælp f.eks. til at visualisere alle løsninger til komplekse ligninger, men er i kurset primært et værktøj som du kan bruge til at checke de beregninger, der indgår i pointopgaverne og den afsluttende eksamen. Især hvis du har erfaring med at du laver mange regnefejl i omfattende beregninger, kan det være godt at checke beregningerne trin for trin i SymPy.
Vi starter med at importere den imaginære enhed ved hjælp af from sympy import I, \(I\) er SymPys standardbetegnelse for det imaginære tal \(i\).
import sympy as sp
from sympy import I, pi
5.12.1. Almindelige regneoperationer med komplekse tal#
Når vi benytter I, får vi automatisk et komplekst tal, og SymPy behandler det som sådan ganske automatisk. Vi kan altså skrive \(z = 3 + 4i\) som z = 3 + 4 * I:
z = 3 + 4 * I
z
Eller vi kan lave et mere generelt udtryk, hvor vi istedet benytter symboler:
from sympy.abc import a, b
w = a + b * I
w
Når vi først har defineret vores udtryk, så kan vi regne med dem på samme måde som med alle andre (reelle) tal. Regneoperationerne +, -, * og / fungerer som de skal.
z = 1 + 2 * I
w = - 3 * I
z + w
z - w
z * w
Ved multiplikation og division er det nogle gange en god idé at bede SymPy om at reducere udtrykket. Især, hvis man gerne vil have det på en \(x + yi\) form:
sp.simplify(z * w)
display(z / w,
sp.simplify(z / w))
Man kan desuden beregne potenser af et kompleks tal på sædvandligvis ved at bruge **:
z ** 3
I dette tilfælde er der ikke meget hjælp at hente i simplify:
sp.simplify(z ** 3)
Vi kan til gengæld bede SymPy om at gange parentesen ud med sp.expand:
sp.expand(z ** 3)
SymPy ved, hvordan den skal håndtere komplekse tal i mange sammenhænge, hvor fortolkningen er entydig. Man kan altså blot bruge komplekse tal i sp.exp(), sp.cos() eller lignende.
5.12.2. Notationsformer og skift mellem disse#
Når vi arbejder med komplekse tal, benytter vi enten kartetiske koordinater eller modulus/argument. I SymPy er der en del metoder til at konverterer den ene eller anden vej, som vi vil gennemgå i dette afsnit.
5.12.2.1. Kartesiske koordinater, real og imaginærdel.#
Funktionerne sp.re() og sp.im() giver real- og imaginærdelen af et komplekst tal. Det er naturligvis trivielt hvis vi starter med et imaginært tal af formen \(x + iy\):
z = 10 - 7 * I
display(z,
sp.re(z),
sp.im(z))
Men det er mere oplysende, hvis vores komplekse tal har en anden form, for eksempel \(4 e^{i \pi / 3}\):
w = 4 * sp.exp(I * pi / 3)
display(w,
sp.re(w),
sp.im(w))
5.12.2.2. Modulus og argument#
Vi kan desuden nemt beregne modulus og argument. Modulus for et komplekst tal er det samme som tallets absolutte værdi (TL s. 126) og findes med sp.Abs(). Bemærk at man bruger et stort A for at adskille kommandoen fra Pythons abs-funktion. For symbolske udtryk vil SymPy dog automatisk bruge sp.Abs() selv hvis vi bruger et lille a. Så for de to tal defineret ovenfor får vi:
display(sp.Abs(z),
sp.Abs(w))
Argumentet findes ved sp.arg() :
display(sp.arg(z),
sp.arg(w))
Hvorefter vi som nævnt tidligere kan bruge .evalf(), hvis vi f.eks. vil have et bud på værdien af \(-\arctan (7/10)\) med fire decimaler
sp.arg(z).evalf(4)
5.12.2.3. Kompleks konjugering#
Vi vil ret ofte benytte os af kompleks konjugering, hvor vi skifter fortegn på imaginærdelen (svarende til at vi spejler i den reelle akse). Dette kan vi gøre ved brug af sp.conjugate(), som virker på imaginære tal uanset notationsform. Bemærk at funktionen hedder det samme som den tilsvarende funktion for matricer, som vi kender fra Lineær Algebra, men som har en anden kaldesekvens:
display(z,
sp.conjugate(z), # Konjugering af komplekst tal
z.conjugate()) # Konjugering af matrix ... men da z kan opfattes som en 1 x 1 matrix, er resultatet det samme
display(w,
sp.conjugate(w))
5.12.3. Rødder og ligninger#
En central egenskab ved de komplekse tal er, at et polynomium af n’te grad altid har netop n rødder (med multiplicitet). Vi skal ofte finde rødder i polynomier og løsninger til ligninger, og her indgår der ofte kvadratrødder og andre rødder af komplekse tal. Se TK 3.4.2 s. 141, hvor det fremgår at der altid er netop \(n\) n’te rødder. Når vi vil finde den n’te rod af et komplekst tal, benytter vi sp.root. Syntaksen er således, at \(\sqrt[n]{z}\) skrives som
sp.root(z, n, hvilken_rod)
hvor hvilken_rod er et tal mellem \(0\) til \(n-1\) (husk at Python tæller fra 0) og fortæller
SymPy, hvilken af de \(n\) rødder, den skal udregne.
z = - 3 + 3 * I
display(z)
sp.root(z, 4, 0)
Dette er utvivlsomt korrekt, men når man ønsker et mere anvendeligt svar, kan man f.eks. tvinge SymPy til at udregne real-delen og imaginærdelen som vi gjorde ovenfor:
r1 = sp.root(z, 4, 0)
display(sp.re(r1))
display(sp.im(r1))
Vi vil nu se på rødderne i et simplere tilfælde, nemlig \(\sqrt[4]{-4}\).
Hvis vi ønsker at finde alle rødderne på en gang og få dem præsenteret i en liste, kan vi enten skrive det op som en ligning:
from sympy.abc import x
display(*sp.solve(sp.Eq(x**4, -4), x))
Eller vi kan beregne rødderne en efter en ved hjælp af en for-løkke:
for i in range(4):
r = sp.root(-4, 4, i)
display(sp.re(r) + I * sp.im(r))
Vi kan finde rødder til polynomier ved hjælp af sp.solve(). Vi minder om at hvis vi kun giver sp.solve() et udtryk (og altså ikke en ligning, f.eks. dannet ved hjælp af sp.Eq), så finder funktionen løsninger til den ligning, der fremkommer når udtrykket sættes lig 0:
from sympy.abc import z
# Definer p som også har imaginære rødder
p = z ** 3 - z ** 2 + 4 * z + -4
# Løs med sp.solve ved hjælp af udtrykket for p, der automatisk sættes lig nul
display(*sp.solve(p))
#... eller med en mindre elegant syntaks, hvor ligningen eksplicit er angivet til z3 - z^2 + 4z = 4
display(*sp.solve(sp.Eq(z**3 - z**2 + 4 * z, 4), z))
5.12.4. Visualisering i det komplekse plan#
Der er ikke et decideret tegneværktøj til komplekse tal i SymPy. Vi tager derfor de to værktøj, som I har set i MekRel frem. NumPy og Matplotlib, da dette langt hen af vejen vil give de mest elegante løsninger. Når vi gør dette vil vi fra numpy importerer array, og så vil vi bruge plot fra Matplotlib. Se eventuelt noterne fra Python i Mekrel.
Når vi først har en liste af komplekse tal i SymPy, kan vi benytte array sammen med nøgleordet dtype = complex til at danne et numerisk numpy-array med komplekse tal.
Når vi først har en liste, kan vi lave lister over real-delene og de komplekse dele med hhv. .real og .imag, og så bruge plot fra matplotlib til at vise dette.
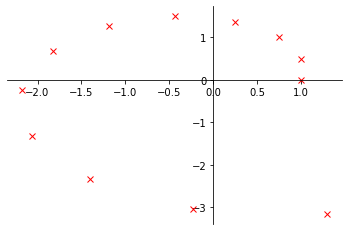
Vi viser her et eksempel, hvor vi visualiserer et komplekst tal opløftet i en stigende potens.
# Vi tager et eksempel med (1 + i/2)^n for n = 0, ..., 11
z = 1 + I/2
# Tom liste
zs = []
for n in range(12): # Vi kører nu igennem tolv gange (altså fra 0 til 11) og tilføjer potensen til en liste
zs.append(sp.expand(z ** n))
display(zs)
[1,
1 + I/2,
3/4 + I,
1/4 + 11*I/8,
-7/16 + 3*I/2,
-19/16 + 41*I/32,
-117/64 + 11*I/16,
-139/64 - 29*I/128,
-527/256 - 21*I/16,
-359/256 - 1199*I/512,
-237/1024 - 779*I/256,
1321/1024 - 6469*I/2048]
Vi kan nu lave zs til et numerisk array ved brug af numpy:
from numpy import array
z_numerisk = array(zs, dtype = complex)
Nu kan vi plotte z_numerisk.real af x-aksen og z_numerisk.imag af y-aksen. Vi importerer Matplotlib til dette formål og kalder plt.plot. Vi fortæller desuden at vi vil have “x” som markeringer og have en rød farve.
import matplotlib.pyplot as plt
plt.plot(z_numerisk.real, z_numerisk.imag, "x", color = "red")
[<matplotlib.lines.Line2D at 0x7f75ce012970>]

Ønsker man at lave plottet med “de klassiske akser”, der krydser hinanden i (0,0), kan man gøre følgende:
# Samme plot som overstående
plt.plot(z_numerisk.real, z_numerisk.imag, "x", color = "red")
# Ryk venstre akse til midten
plt.gca().spines['left'].set_position("zero")
# Skjul den højre
plt.gca().spines['right'].set_color(None)
# Gentag for nederste og toppen
plt.gca().spines['bottom'].set_position("zero")
plt.gca().spines['top'].set_color(None)